| 我们知道,两端铰支、中心受压的细长杆的欧拉临界力为: |
|
|
|
式中, L 为压杆的长度, I min 为截面的最小惯性矩。当压杆所受的荷载 P 小于试件的临界力 Pcr 时,中心受压的细长杆在理论上应保持直线形状,杆件处于稳定平衡状态。当 P ≥Pcr 时,杆件因丧失稳定而弯曲。若以荷载 P 为纵坐标,压杆中点挠度 f 为横坐标,按小挠度理论绘出的 P-f 图形如图6.4所示。
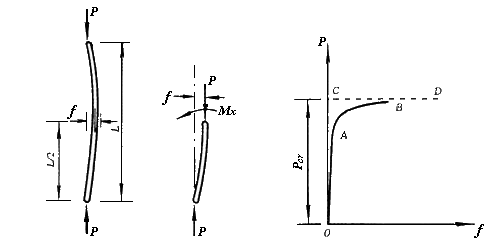
图6.4 中心压杆内力分析及其临界压力
由于试件可能有初曲率,压力可能偏心,以及材料的不均匀等因素,实际的压杆不可能完全符合中心受压的理想情况。在实验过程中,即使压力很小时,杆件也会发生微小弯曲,中点挠度随荷载的增加而逐渐增大。若令杆件轴线为X坐标轴,杆件下端点为坐标轴原点,则在x=L/2处截面上(图6.4)的弯矩和轴力为:
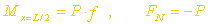
| |
横截面上的最大/最小正应力为: |
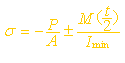 |
|
当用半桥温度自补偿的方法将电阻应变片接到静态电阻应变仪后,可消除由轴向力产生的应变读数,这样,应变仪上的读数就是测点处由弯矩 M 产生的弯曲正应变的两倍,把应变仪读数写为εds ,把弯曲正应变写为ε ,则 εds=2ε。相应弯曲正应力为:
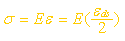
| 从上述两式便可导出压杆挠度f 与应变仪读数εds的关系式: |
|
|
|
由上式可见,在一定的荷载P作用下,应变仪读数εds 的大小反映了压杆挠度 f 的大小,εds 越大,表示 f 越大。所以用电测法测定 Pcr 时,图6.4的横坐标 f 可用εds 来代替。当P远小于 P c r 时,随着荷载的增加εds 也随之增加,但增长极为缓慢( OA 段);而当 P 趋近于临界力 Pcr 时,虽然荷载增加量不断减缓,但εds 却会迅速增大( AB 段),曲线 AB 是以直线 CD 为渐近线的。试件的初曲率与偏心等因素的影响越小,则曲线 OAB 越靠近折线OCD。所以,可根据渐近线 CD 的位置确定临界荷载 Pcr 。
|