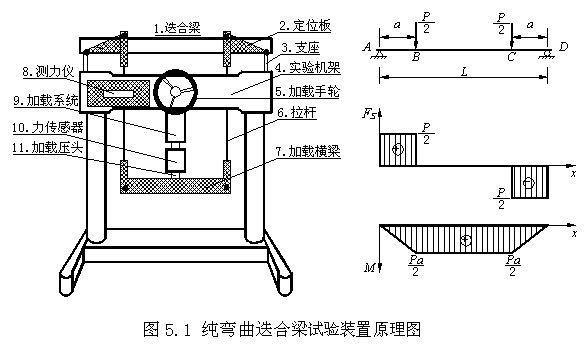
叠合梁弯曲实验装置（图5.1-左）组成包括：叠合梁（工作梁）、定位板、支座、试验机架、加载系统、两端万向接头的加载拉杆、加载压头（Φ16 的球形钢珠）、加载横梁、载荷传感器和测力仪等组成。实验装置的工作梁是一根已粘贴好应变片的叠合梁。叠合梁由铝-钢两种材料层粘接而成，我们通常称为铝-钢叠合梁。实验装置采用转动手轮加载的方法，载荷大小由与载荷传感器相连接的测力仪显示。每增加载荷增量 ，通过两根加载拉杆传递到钢梁（距两端支座分别为a 的作用点） 。

当加载手轮转动至P 时，铝-钢叠合梁的 B 、C 处分别受到垂直向下的力，大小均为P/2，BC 段剪力图恒为零，即BC 段梁属于纯弯曲段，其弯矩为M=Pa/2。工作梁的受力简图、剪力图及弯矩图如图5.1右侧所示。

已知叠合梁纯弯曲正应变、弯曲正应力的理论公式为：

（5-1）

公式（5-1）表明叠合梁整个横截面上的正应变沿y成线性分布，但叠合梁不同材料层横截面上的正应力沿y却成分段线性分布。为了验证（5-1）理论公式的正确性，在工作梁纯弯曲段的侧面，沿不同的高度粘贴了电阻应变片，应变测量方向均平行于梁轴，布片方案及各应变片编号见图5.2 所示。当梁加载变形时，利用电阻应变仪测出各应变片的应变值，然后根据单向应力状态的虎克定律求出不同材料层各点实测的应力值。

（5-2）

式中: E1、E2 为叠合梁不同材料层的弹性模量； ε实　为电阻应变仪测量的应变值。将测得的应力值与理论应力值进行比较，从而验证叠合梁弯曲正应力理论公式的正确性。

由于式（ 5-1 ）、式（ 5-2 ）只适用于材料的比例极限以内， 故工作梁的加载必须在此范围内进行。为了随时观察变形与载荷的线性关系，实验时采用逐次增量法加载，即每增加等量载荷△ P ， 测读各点的应变一次，观察各次的应变增量是否也基本相同。然后，再重复上述加载过程（从零至最终载荷）两次，以便了解应变测量数据的重复性如何。尽管应变片是按叠合梁形心层上下对称布置的，但中性层已经不再是形心层——试观察叠合梁应变值的分布规律。最后，取三次最终载荷所测得的应变平均值计算各点的应力值 σ实 。

本实验电阻应变片连接采用半桥温度补偿接法。考虑到12个应变片所在测量点的温度条件基本相同，为方便测量，12个应变片共用一片温度补偿片，即公共补偿片法。