理论分析

当竖向荷载 P 作用在加力杆 C 点时，试件 AB 发生弯曲与扭转组合变形 (见"实验介绍"图4.2)， B 、 D 点所在截面的内力有弯矩 M 、剪力 Q 和扭矩 M r 。因此该横截面上同时存在弯曲引起的正应力 Q w ，扭转引起的剪应力τT ( 弯曲引起的剪应力比扭转引起的剪应力小得多，故在此不予考虑 ) 。根据弯矩引起的正应力和扭转引起的剪应力在该截面上的分布规律，从 B 、 D 两点截取单元体，其各面上作用的应力为：

显然， B 、 D 两点均处于平面应力状态。根据应力状态理论，该两点的主应力大小和方向由以下两式决定：

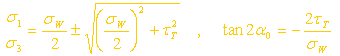
测试原理

为了用实验的方法测定薄壁圆管弯曲和扭转时表面上一点处的主应力大小和方向，首先要在该点处测量应变，确定该点处的主应变ε 1 ，ε 3 的数值和方向，然后利用广义胡克定律算得主应力б 1 ，б 3 。根据应变分析原理，要确定一点处的主应变，需要知道该点处沿 x,y 两个相互垂直方向的三个应变分量ε x ，ε y ，γ xy 。由于在实验中测量剪应变很困难，而用电阻应变片测量线应变比较方便，所以，通常采用测量一点处沿着与轴成三个已知方向的线应变ε a ，ε b ，ε c 的方法（图4.3），按下列方程组联立求得ε x ，ε y ，γ xy ：

（4-3）

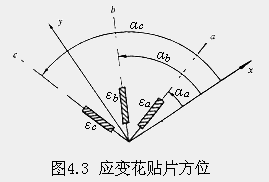
为了简化计算，往往采用互成特殊角度的三片应变片组成的应变花，本实验用了 45° 应变花，将其粘贴在测点 A 、 B 、 C 、 D 处（见"实验介绍"图 4.2）。通过电阻应变仪可测得这些点处沿与杆轴线 x 轴成 -45°， 0°， 45°三个方向的线应变ε_-45°，ε_0°，ε_45°。借助方程式（4-3 ）以及主应变转轴公式，可获得主应变的数值为：

（4-4）

主应变的方向为：

（4-5）

注意：αo 为 x 轴到主应变方向的夹角，以逆时针转向为正。

利用广义胡克定律可导出主应力的大小为：

（4-6）

其中主应力方向与主应变方向一致。综上所述，通过电阻应变仪测得的弯扭圆轴各测点沿 -45° ， 0° ， 45°三个方向的线应变ε_-45°，ε_0°，ε_45°测量值，最终可以得到被测点的主应力大小和方向。